Прием: конвертация из декартовой системы координат

На практике можно столкнуться с задачей: перенести векторный рисунок, созданный в декартовой системе координат, в SVG. В декартовой системе координат, точка (0, 0) находится в нижнем левом углу холста, а у-координаты возрастают по мере движения вверх.

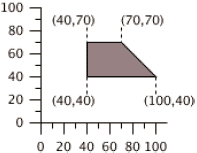
Выходит ситуация, когда ось-у перевернута вверх ногами по отношению к системе SVG. Чтобы рисунок отобразился в SVG так же как и в исходной системе, координаты необходимо пересчитать. Чтобы не делать это вручную, можно воспользоваться последовательностью трансформаций, чтобы SVG сам все сделал. Для этого, сначала, просто переносим картинку в SVG с исходными координатами. Для большей наглядности нарисуем оси декартовой системы координат. Результат предсказуем — рисунок получился перевернутым вверх ногами.

<svg width="200px" height="200px" viewBox="0 0 200 200">
<!-- оси -->
<line x1="0" y1="0" x2="100" y2="0" style="stroke: black;"/>
<line x1="0" y1="0" x2="0" y2="100" style="stroke: black;"/>

<!-- трапеция-->
<polygon points="40 40, 100 40, 70 70, 40 70" style="fill: gray; stroke: black;"/>
</svg>

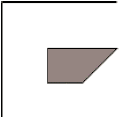
Чтобы закончить конвертацию, выполняем следующие шаги:

1. Находим максимальную y-координату (max-y). В данном случае она будет равна 100 (конец линии, изображающей ось y).
2. Помещаем весь рисунок в элемент <g>.
3. Делаем перемещение системы координат вниз на максимальное значение y-координаты: transform=»translate(0, max-y)».
4. Переворачиваем вверх ногами ось y с помощью трансформации scale со значением «-1″ для оси y: transform=»translate(0, max-y) scale(1, -1)».

<svg width="200px" height="200px" viewBox="0 0 200 200">
<g transform="translate(0,100) scale(1,-1)">
	<!-- оси -->
	<line x1="0" y1="0" x2="100" y2="0" style="stroke: black;"/>
	<line x1="0" y1="0" x2="0" y2="100" style="stroke: black;"/>

	<!-- трапеция -->
	<polygon points="40 40, 100 40, 70 70, 40 70" style="fill: gray; stroke: black;"/>
</g>
</svg>

Результат в живуюили смотрим на картинке:>

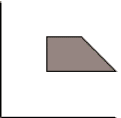
Куда дальше

• следующая — Трансформация в SVG: поворот
• предыдущая — Последовательность трансформаций в SVG
• содержание